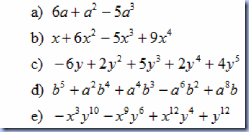Algebra Baldor: Preliminares - Ejercicio 6
Algebra Baldor con Ejercicios Solucionados

CLASIFICACIÓN DE LAS EXPRESIONES ALGEBRAICAS
24. CLASES DE POLINOMIOS
Un polinomio es entero cuando ninguno de sus términos tiene denominador literal.fraccionario cuando alguno de sus términos tiene letras en el denominador
racional cuando no contiene radicales
irracional cuando contiene radical
homogéneo cuando todos sus términos son del mismo grado absoluto
y heterogéneo cuando sus términos no son del mismo grado
25. ORDENAR UN POLINOMIO
es escribir sus términos de modo que los exponentes de una letra escogida como letra ordenatriz queden en orden descendente o ascendente .
26. TÉRMINO INDEPENDIENTE DE UN POLINOMIO CON RELACIÓN A UNA LETRA
es el término que no tiene dicha letra .
EJERCICIO 6

6. Clases de polinomios
Solución de los Ejercicios
1. Atendiendo a si tienen o no denominador literal y a si tienen o no radical, dígase qué clase son los polinomios siguientes:
2. Escribir un polinomio de tercer grado absoluto; de quinto grado absoluto; de octavo grado absoluto; de décimo quinto grado absoluto.
Definición: "El grado absoluto de un polinomio es el grado de su término de mayor grado absoluto".

3. Escribir un trinomio de segundo grado respecto de la x; un polinomio de quinto grado respecto de la a; un polinomio de noveno grado respecto de la m.

4. De los siguientes polinomios:

escoger dos que sean homogéneos y dos hetereogéneos.
S o l u c i ó n :
Definición 1: "Un polinomio es homogéneo cuando todos sus términos son del mismo grado absoluto".
Definición 2: "Un polinomio es heterogéneo cuando sus términos no son del mismo grado absoluto".
Definición 3: "El grado absoluto de un término es la suma de los exponentes de sus factores literales".
Los polinomios homogéneos serían: a) y e)
{en (a) todos los términos son de tercer grado absoluto, y en (e) todos los términos son de quinto grado absoluto}.
Los polinomios heterogéneos serían: c) y d).
5. De los siguientes polinomios:

dígase cuáles son completos y respecto de cuáles letras.
S o l u c i ó n :
El polinomio (a) es completo respecto a la a.
El polinomio (c) es completo respecto a la y.
El polinomio (e) es completo respecto a la b y a la y.
6. Escribir tres polinomios homogéneos de tercer grado absoluto; cuatro de quinto grado absoluto; dos polinomios completos.
S o l u c i ó n :

7. Ordenar los siguientes polinomios respecto de cualquier letra en orden descendente:

S o l u c i ó n :

8. Ordenar los siguientes polinomios respecto de cualquier letra en orden ascendente:

S o l u c i ó n :