Gwanggaeto el grande › Perros en el mundo antiguo » Orígenes e Historia
Artículos y Definiciones › Contenido
- Gwanggaeto el grande › Quien fue
- Perros en el mundo antiguo › Orígenes antiguos
Civilizaciones antiguas › Lugares históricos y sus personajes
Gwanggaeto el grande › Quien fue
Definición y orígenes

Gwanggaeto (Kwanggaeto), a menudo referido como Gwanggaeto el Grande, era el rey del reino de Goguryeo ( Koguryo ) que gobernó el norte de Corea durante el período de los Tres Reinos. Gwanggaeto reinó entre los años 391 y 413 EC, y cumpliendo con su otro título de 'amplio expansor de dominio', extendió el reino en su mayor extensión y presidió el período de mayor prosperidad. Su duradera reputación como uno de los mejores líderes y comandantes de campo de Corea se debe en gran parte a una larga estela inscrita que se encuentra fuera de su enorme tumba en la entonces capital de Kungnaesong, Goguryeo.
PERÍODO DE ORO DE GOGURYEO
El reino de Goguryeo gobernó desde el 37 aC hasta el 668 dC y fue el más grande de los tres reinos de la antigua Corea. No fue hasta el siglo IV EC que el estado desplegó un gobierno totalmente centralizado y control de su territorio. Luego, a principios del siglo V de nuestra era, comenzó el período más grande de Goguryeo durante el reinado de Gwanggaeto. Una sólida base política en el país aliada con relaciones extranjeras pragmáticas con los vecinos de Goguryeo Baekje ( Paekche ) y Silla fue mano a mano con una agresiva política expansionista hacia las tribus del norte y los estados del sur de China. Al mismo tiempo, se mantuvieron relaciones amistosas con los estados del norte de China. El resultado de esta mezcla de militarismo y diplomacia fue que Gwanggaeto finalmente pudo dominar Corea del Norte, la mayor parte de Manchuria y una parte de Mongolia Interior. Goguryeo también se benefició de esta prosperidad con Gwanggaeto construyendo nueve nuevos templos budistas solo en Pyongyang. Tan exitoso fue este período que Gwanggaeto incluso acuñó un nuevo término para él: Yongnak o "Eterno regocijo".
TAN EXITOSO FUE EL REINADO DE GWANGGAETO QUE INCLUSO COINCINO UN NUEVO TÉRMINO PARA ELLO: YONGNAK O 'REGOCIMIENTO ETERNO'.
ESTELA DE GWANGGAETO
Gran parte de lo que se conoce de la historia de este período proviene del sag Samguk del siglo XII. texto ('Registros históricos de los tres estados') y una estela de 7.3 metros de alto erigida fuera de la tumba de Gwanggaeto por su hijo Changsu en 414 CE. La piedra grabada relata las hazañas del rey en 1,800 caracteres de escritura de sellos chinos. La estela es la inscripción más antigua conocida de la antigua Corea y es un registro histórico extraordinario de los principales acontecimientos del reinado de Gwanggaetto. El texto comienza describiendo la base de Goguryeo por el legendario Chumong. Hay una cita del texto clásico confuciano Shujing y una referencia al rey por el título del reino chino Yongnak. Esto último es significativo ya que otorga a Gwanggaetto el mismo estatus que el emperador chino, que era la única persona a la que se le permitía un título de reinado.
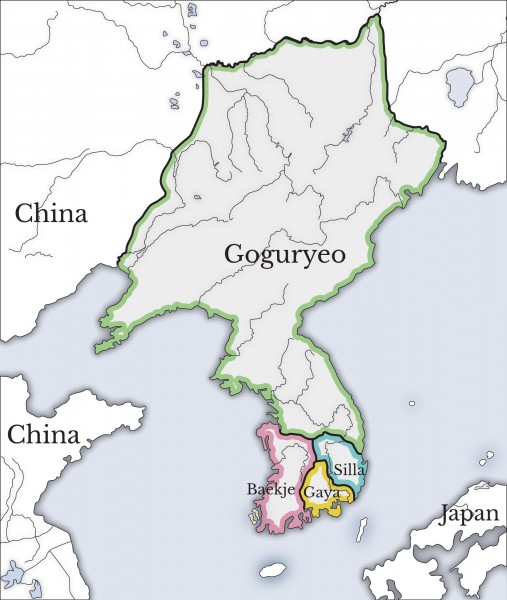
Tres reinos de Corea
El texto continúa describiendo el acceso de Gwanggaeto al trono cuando tenía 19 años, y luego hay una larga lista de sus hazañas militares. Al reformar las fuerzas armadas de Goguryeo en unidades navales, de ejército y de caballería separadas, el rey asumió un puesto al frente de una cadena de mando centralizada y condujo personalmente a sus hombres en el campo. También hubo desarrollos en este momento en la forja de metal para que los guerreros de Goguryeo tuvieran armas de acero superiores. Con una unidad de caballería blindada, ocupó la fortaleza Liaodong en el sureste de Manchuria, conquistó las tribus Murong, Sushen (Sukchin) y Yilou del norte, y capturó áreas del reino rival de Baekje al suroeste en 396 CE, incluida brevemente la capital Hansong, la fortaleza de Gwanmiseong, y la cuenca del río Han estratégicamente importante. El rey Baekje Asin ahora tomó sus órdenes de Gwanggaeto.
Con el apoyo militar de Gwanggaeto de 50,000 hombres, el reino de Silla fue capaz de repeler con éxito una fuerza de invasión japonesa Wa y Baekje en 400 CE. De hecho, el reino de Silla bajo el reinado de Namul se convirtió en un vasallo de Goguryeo. También en 400 CE Goguryeo y Silla se unieron de nuevo, esta vez para atacar la pequeña confederación Gaya ( Kaya ) en el extremo sur de la península. Esta alianza entre Goguryeo y Silla puede explicar la presencia de un cuenco de bronce con tapa con el nombre de Gwanggaeto, que fue descubierto en una tumba en la capital de Silla, Gyeongju (Kyongju).En efecto, Goguryeo, aunque vagamente, ahora controla la mayor parte de Corea.
En 406 CE se firmó un tratado de paz con el estado de Murong Later Yan en el que Goguryeo se vio obligado a prestar ayuda militar contra el estado de Tuoba Northern Wei de China a cambio de ganancias territoriales. Cerca del final de su reinado en 410 EC la mayoría de Manchuria y la zona de la costa este vecina, conocida como la Provincia Marítima de Rusia, estaban bajo el control de Goguryeo. La estela también afirma que el rey conquistó no menos de 64 ciudades fortificadas y 1.400 aldeas, de modo que cuando murió, Goguryeo controlaba dos tercios de la península de Corea y una amplia franja de Manchuria.

Gwanggaeto Stele
La estela no está exenta de controversia. Desapareció durante siglos y solo volvió a aparecer en la década de 1880, cuando, afortunadamente, un soldado japonés rozó el texto. La porción del texto estelar que describe la victoria de Gwanggaeto sobre los japoneses fue destrozada durante la ocupación japonesa en el siglo XX. Los historiadores japoneses sostienen que la estela corrobora la teoría de que Japón tenía una colonia en el sudeste de Corea del 365 al 561 dC, pero esto es controvertido.
MUERTE Y TUMBA
Gwanggaeto murió en 413 EC y fue sucedido por su hijo Changsu quien, increíblemente, reinó hasta el año 491 dC, lo que le valió el merecido título de 'longevo'. Continuó el trabajo de su padre, movió la capital de Kungnaesong a Pyongyang en 427 CE y aseguró la prosperidad continua de Goguryeo.
Desde el siglo IV EC, los reyes de Goguryeo fueron enterrados en tumbas construidas con bloques de piedra tallada dentro de grandes montículos de tierra. El mayor ejemplo de tal tumba se encuentra en la antigua capital Kungnaesong (la moderna Tonggou / Tungkou) y se cree que es la de Gwanggaeto. También se conoce como la Tumba del General. Con 75 metros de largo y usando bloques que miden hasta 3 x 5 metros, tiene cuatro estructuras más pequeñas tipo dolmen en cada esquina.La estela que proclama las obras del gran rey está justo afuera.
Este artículo fue posible gracias al generoso apoyo de la Sociedad Coreana Británica.
Perros en el mundo antiguo › Orígenes antiguos
Civilizaciones antiguas
Los perros han sido parte de la historia de los seres humanos desde antes de la palabra escrita. El antiguo templo de Gobekli-Tepe en Turquía, datado de al menos 12,000 años aC, ha proporcionado a los arqueólogos evidencia de perros domesticados en el Medio Oriente que corresponden a la evidencia más temprana de domesticación, la tumba de Natufian, (aproximadamente 12,000 aC) descubierta en Ein Mallaha, Israel, en el que un anciano fue enterrado con un cachorro. En muchas culturas en todo el mundo antiguo, los perros ocuparon un lugar destacado y, en gran medida, se los consideró de la misma manera que lo son en la actualidad. Los perros fueron vistos como fieles compañeros, cazadores, guardianes y como una parte atesorada de la familia.

Mosaico de perro
PERROS EN MESOPOTAMIA
En la historia más antigua del Cercano Oriente, La epopeya de Gilgamesh de la antigua Mesopotamia (fechada entre 2150y 1400 aC), los perros aparecen en un papel destacado como acompañantes de una de las diosas más populares de la región; la diosa Innana ( Ishtar ) viaja con siete preciados perros de caza con collar y correa. Aunque a Egipto se le atribuye la invención del collar de perro, lo más probable es que se haya desarrollado en Sumer. Se puede suponer que el desarrollo del collar de perro se sugirió poco después de que los perros fueron domesticados, lo que sucedió en Mesopotamia antes de Egipto. Se encontró un colgante dorado de un perro (claramente un Suluki) en la ciudad sumeria de Uruk, fechada en 3300 aC, y un sello cilíndrico de Nínive (fechado hacia el 3000 aC) también presenta un Saluki. El colgante para perro usa un collar ancho; evidencia del collar de perro en uso en ese momento.
En el famoso Descendimiento de Innana (una historia considerada más antigua y que no forma parte de Gilgamesh ) en la que la diosa desciende al inframundo, su esposo, Dumuzi, tiene perros domesticados como parte de su séquito real. Perros destacados en la vida cotidiana de los mesopotámicos. El historiador Wolfram Von Soden lo nota, escribiendo :
El perro (nombre sumerio, ur -gi ; nombre semítico, Kalbu ) fue uno de los primeros animales domésticos y se utilizó principalmente para proteger rebaños y viviendas contra los enemigos. A pesar del hecho de que los perros vagaban libremente por las ciudades, el perro en el antiguo Oriente estaba generalmente vinculado a un solo amo y era cuidado por él. Por supuesto, el perro también era un carroñero, y en las aldeas proporcionaba el mismo servicio que las hienas y los chacales. Por lo que podemos decir, solo había dos razas principales de perros: grandes galgos que se usaban principalmente en la caza y perros muy fuertes (del orden de los daneses y los mastines), que en el antiguo Oriente eran más que suficientes para los lobos generalmente más pequeños y, por esa razón, eran especialmente adecuados como perros de rebaño. Las fuentes distinguen numerosas subrazas, pero solo podemos identificarlas parcialmente. El perro a menudo era el compañero de los dioses de la terapéutica. Aunque se produjo la expresión "perro feroz", se usó poco el término "perro" como un término peyorativo (91).

Cazadores asirios con perros
Los perros se representan en el arte de Mesopotamia como cazadores, pero también como compañeros. Los perros fueron mantenidos en el hogar y fueron tratados de la misma manera por las familias que los cuidan como lo están hoy. Las inscripciones y las placas con incrustaciones representan a los perros que esperan a sus amos y, según el historiador Bertman, incluso escuchan su música maestra: "Las imágenes en placas incrustadas, piedras de sello talladas y relieves esculpidos nos transportan hacia atrás... Vemos una el pastor toca su flauta mientras su perro se sienta y escucha atentamente "(294). Los perros protegieron el hogar y se llevaron imágenes amistosas de caninos, como la mencionada anteriormente de Uruk, para su protección personal. Los famosos Perros Nimrud, figuritas de arcilla de caninos que se encuentran en la ciudad de Kalhu, fueron enterrados debajo o al lado del umbral de los edificios por su poder protector. Se recuperaron otras cinco estatuillas de perro de las ruinas de Nínive y las inscripciones relatan cómo estas figurillas estaban imbuidas del poder del perro para protegerse del peligro. Además, las referencias de "dioses de la terapéutica" de Von Soden arriba fueron las deidades involucradas con la salud y la curación y, más notablemente, la diosa Gula que fue representada regularmente en presencia de su perro. La saliva de perro se consideró medicinal porque se observó que, cuando los perros lamían sus heridas, promovía la curación.
EL PERRO EN LA INDIA
En la India antigua, el perro también era muy apreciado. El perro indio paria, que todavía existe hoy, es considerado por muchos como el primer perro verdaderamente domesticado en la historia y el más antiguo del mundo (aunque esto ha sido cuestionado). La gran epopeya cultural El Mahabharata (alrededor del 400 aC) presenta un perro que puede haber sido uno de estos perros parias. La epopeya relata, hacia el final, la historia del Rey Yudisthira, muchos años después de la Batalla de Kurukshetra, haciendo una peregrinación a su lugar de descanso final. En el camino, es acompañado por su familia y su fiel perro. Uno por uno, los miembros de su familia mueren a lo largo del sendero, pero su perro permanece a su lado. Cuando, por fin, Yudisthira llega a las puertas del paraíso, es bienvenido por la buena y noble vida que ha vivido, pero el guardián de la puerta le dice que el perro no puede entrar. Yudisthira se sorprende de que una criatura tan leal y noble como su perro no se le permita entrar en el cielo y por lo tanto decide quedarse con su perro en la tierra, o incluso ir al infierno, que entrar en un lugar que excluiría al perro. El guardián en la puerta le dice a Yudisthira que esta era solo una última prueba de su virtud y que, por supuesto, el perro también puede entrar. En algunas versiones de este cuento, el perro se revela como el dios Vishnu, el conservador, que ha estado vigilando a Yudisthira toda su vida, vinculando así la figura del perro directamente con el concepto de dios.
EGIPTO Y EL PERRO
La conexión del perro con los dioses y la lealtad del perro a los seres humanos se explora más a fondo en otras culturas. En el antiguo Egipto, el perro estaba vinculado al dios chacal-perro, Anubis, quien guiaba el alma del difunto al Salón de la Verdad, donde el gran dios Osiris juzgaría al alma. Los perros domesticados fueron enterrados con gran ceremonia en el templo de Anubis en Saqqara y la idea detrás de esto parecía ser ayudar a los perros fallecidos a pasar fácilmente al más allá (conocido en Egipto como el Campo de juncos) donde podían continuar disfrutando de su vive como lo hicieron en la tierra.
El perro más conocido honrado de esta manera es Abuwtiyuw quien fue honrado con un gran entierro en el Antiguo Reino(c.2613-2181 a. C.) cerca de la meseta de Giza. Abuwtiyuw era el perro de un sirviente desconocido del rey, (cuya identidad tampoco está clara) cuya losa de piedra caliza fue descubierta en 1935 CE por el egiptólogo George Reisner. La losa inscrita habría sido una vez parte de la capilla conmemorativa del propietario y relata cómo "Su Majestad ordenó que él [el perro] sea sepultado ceremonialmente, que se le dé un ataúd del tesoro real, lino fino en gran cantidad e incienso. "
LOS PERROS FUERON ALTAMENTE VALORADOS EN EGIPTO COMO PARTE DE LA FAMILIA Y, CUANDO UN PERRO MORIRÍA, LA FAMILIA, SI PODRÍAN DECIDIRLE, HABRÍA QUE EL PERRO MOMENTADO.
Aunque Abuwtiyuw fue especialmente honrado, los perros en general fueron muy apreciados en Egipto como parte de la familia y, cuando un perro moría, la familia, si podían permitírselo, tendrían al perro momificado con tanto cuidado como pagarían por él. un miembro humano de la familia. Se manifestó un gran dolor por la muerte de un perro de la familia y la familia afeitaría sus cejas como una señal de este dolor (como también lo hicieron con sus gatos). Las pinturas de tumbasdel faraón Ramsés el Grande lo representan con sus perros de caza (presumiblemente en el Campo de juncos) y los perros a menudo fueron enterrados con sus amos para proporcionar este tipo de compañía en la otra vida. La relación íntima entre los perros y sus amos en Egipto se pone de manifiesto a través de las inscripciones que se han conservado:
Incluso conocemos los nombres de muchos perros egipcios antiguos de cuellos de cuero, así como estelas y relieves. Incluyeron nombres como Brave One, Reliable, Good Herdsman, North-Wind, Antelope e incluso "Inútil". Otros nombres provienen del color de los perros, como Blacky, mientras que a otros perros se les dieron números para nombres, como "el quinto". Muchos de los nombres parecen representar cariño, mientras que otros transmiten simplemente las habilidades o capacidades de los perros. Sin embargo, incluso como en los tiempos modernos, podría haber connotaciones negativas para los perros debido a su naturaleza como sirvientes del hombre. Algunos textos incluyen referencias a prisioneros como "el perro del rey" (TourEgypt.com).
El perro como sirviente fue claramente representado a través de estos collares que habrían servido para entrenar y controlar a los animales. La evidencia más antigua del collar de perro en Egipto es una pintura mural fechada c. 3500 a. C. de un hombre paseando a su perro con una correa. La correa parece ser una simple cuestión de una cuerda o tela atada al cuello.Los collares de perro egipcios se fabricaban con una sola pieza de cuero cosida y pegada para formar un anillo que luego se deslizaba sobre la cabeza del perro. A partir de simples anillos de cuero, el collar se volvió más elaborado en el diseño en el momento del Imperio Medio (2040-1782 a. C.) cuando estaban adornados con pernos de cobre o bronce. En el Reino Nuevo (1570-1069 a. C.) estaban aún más atados con elaborados grabados. Esto se ve más claramente en el collar de perro de la tumba de Maiherpri, un noble bajo el reinado de Thutmosis IV (1400-1390 aC) que es una banda de cuero adornada con caballos y flores de loto y teñida de un rosa pálido.
PERROS EN LA ANTIGUA GRECIA
Claramente, el perro era una parte importante de la sociedad y cultura egipcia, pero lo mismo era cierto de la Grecia antigua.El perro era el compañero, protector y cazador de los griegos, y el cuello con pinchos, tan conocido hoy en día, fue inventado por los griegos para proteger los cuellos de los lobos de sus amigos caninos. Los perros aparecen en la literatura griegadesde el principio en la figura del perro de tres cabezas Cerbero que custodiaba las puertas del Hades. Un ejemplo de esto en el arte es el florero Caeretan de figura negra de Heracles y Cerbero de c. 530-520 BCE (actualmente en el Museo del Louvre en París, Francia). En Grecia, como en la antigua Sumeria, el perro se asoció con deidades femeninas en el sentido de que tanto las diosas Artemisa como Hecate tenían perros (Artemisa, perros de caza, mientras que Hécate tenía perros molosos negros).

Estatua de Hades y Cerberus
La escuela filosófica de cinismo en la antigua Grecia toma su nombre del griego para "perro" y los que siguieron esta escuela fueron llamados Kynikos (como perros) en parte debido a su determinación de seguir un camino único lealmente sin desviarse. El gran filósofo cínico Antístenes enseñó en un lugar conocido como Cynosarges (el lugar del perro blanco) y esta, quizás, es otra razón para su nombre.
Los perros también aparecen en el famoso diálogo de República de Platón. En el Libro II, Sócrates afirma que el perro es un verdadero filósofo porque los perros "distinguen el rostro de un amigo y de un enemigo solo por el criterio de saber y no saber" y concluye que los perros deben ser amantes del aprendizaje porque determinan lo que me gusta y lo que no basan en el conocimiento de la verdad. El perro ha aprendido quién es un amigo y quién no y, en función de ese conocimiento, responde de manera adecuada; mientras que los seres humanos a menudo son engañados sobre quiénes son sus verdaderos amigos.
Sin embargo, la historia de perro más famosa de la Grecia antigua es la de Argos, el amigo leal del rey Odiseo de Ithaka del Libro 17 de la Odisea de Homero (c. 800 aC). Odiseo vuelve a casa después de estar ausente durante veinte años y, gracias a la ayuda de la diosa Atenea, no es reconocido por los pretendientes hostiles que intentan ganar a la esposa de Odiseo, la mano de Penélope en matrimonio. Argos, sin embargo, reconoce a su maestro y se levanta de donde ha estado esperando fielmente, meneando la cola en señal de saludo. Odiseo, disfrazado, no puede reconocer el saludo por temor a revelar su verdadera identidad frente a los pretendientes y por lo tanto ignora a su viejo amigo; y Argos vuelve a acostarse y muere. En esto, como en la historia en El Mahabharata, la lealtad del perro se representa de la misma manera. Aunque separados por diferentes culturas y cientos de años, el perro es representado como la figura leal y devota de su maestro, ya sea que el maestro devuelva la devoción o no.
PERROS EN ROMA
En la antigua Roma, el perro se veía de la misma manera que en Grecia y el mosaico conocido, Cave Canem (Cuidado con el perro) muestra cómo los perros fueron apreciados en Roma como guardianes de la casa al igual que en las culturas anteriores y todavía están hoy. El gran poeta latino Virgil escribió: "Nunca, con los perros en guardia, te tienes que tener miedo por tus puestos, un ladrón de medianoche" (Georgics III, 404ff) y el escritor Varro, en su trabajo sobre la vida en el campo, dice que cada familia debe tener dos tipos de perro, un perro de caza y un perro guardián ( De Re Rustica I.21). Los perros protegen a las personas no solo de animales salvajes y ladrones, sino también de amenazas sobrenaturales. La diosa Trivia (la versión romana del griego Hécate) era la Reina de los Espectros, encrucijadas embrujadas y cementerios, y estaba asociada con la brujería. Robaba silenciosamente a la gente para atacarlos, pero los perros siempre la conocían primero; se pensaba que un perro que parecía ladrar a la nada advertía a uno contra el acercamiento de Trivia o algún otro espíritu incorpóreo.
Los romanos tenían muchas mascotas, desde gatos hasta simios, pero favorecían al perro por encima de todos los demás. El perro aparece en mosaicos, pinturas, poesía y prosa. El historiador Lazenby escribe:
Hay una gran serie de relieves griegos y romanos que muestran a hombres y mujeres con sus compañeros caninos. Los relieves gálicos muestran especialmente un toque notablemente humano en las escenas que representan a este favorito de la casa con sus dueños. En estos vemos imágenes encantadoras de una infancia sana y feliz: un niño recostado en un sofá y dando a su perro mascota su plato para lamerlo; otra vez, una niña pequeña, Graccha, quien, según nos dice la inscripción, vivió solo 1 año y 4 meses, tiene en su mano izquierda una canasta que contiene tres cachorros, cuya madre los mira con mucha preocupación (1).
Los perros se mencionan en el código de la ley romana como guardianes del hogar y las bandadas. En un caso que fue registrado, un agricultor presenta una demanda contra su vecino porque los perros del vecino rescataron a los cerdos del granjero de los lobos y el vecino luego reclamó la propiedad de los cerdos. La queja, que se resolvió a favor del agricultor, dice:
Los lobos se llevaron algunos cerdos de mis pastores; el arrendatario de una granja contigua, habiendo perseguido a los lobos con perros fuertes y poderosos, que guardó para la protección de sus rebaños, se llevó a los cerdos lejos de los lobos, o los perros los obligaron a abandonarlos. Cuando mi pastor reclamó los cerdos, surgió la pregunta de si se habían convertido en propiedad de aquel que los recuperó o si aún eran míos, ya que habían sido obtenidos por un cierto tipo de caza (Nagle, 246).
Varro afirmó que ninguna granja debería estar sin dos perros y que deberían mantenerse en el interior durante el día y dejarse vagar por la noche para evitar tal posibilidad como la que se discutió anteriormente. También sugirió que se eligiera un perro blanco sobre uno negro para poder distinguir entre el perro y el lobo en la oscuridad o el ocaso de la mañana.

Perro de cerámica chino
EL PERRO EN CHINA
La antigua China tenía una relación interesante con el perro. Los perros fueron los primeros animales domesticados en China (alrededor de 12,000 aC) junto con los cerdos y fueron utilizados en la caza y se mantuvieron como compañeros. También se usaron, desde el principio, como fuente de alimento y como sacrificio. Los huesos antiguos de los oráculos (que eran los huesos de los animales o las conchas de las tortugas usadas para contar el futuro) mencionan a los perros repetidamente como buenos y malos presagios, dependiendo de cómo, en qué condiciones y en qué circunstancias se observó al perro.
La sangre de un perro era un componente importante para sellar juramentos y jurar lealtades porque se pensaba que los perros se habían dado a los humanos como un regalo del cielo y por lo tanto su sangre era sagrada. Como un regalo de lo divino, fueron honrados, pero se entendió que habían sido provistos para un propósito: ayudar a los seres humanos a sobrevivir proporcionándoles comida y sangre para el sacrificio.
Los perros fueron asesinados y enterrados una vez en el frente de una casa, o antes de las puertas de la ciudad, para evitar la enfermedad o la mala suerte. Con el tiempo, los perros de paja reemplazaron a los perros reales a medida que la práctica de sacrificar a los perros se hizo menos popular. La enfermedad o la mala suerte que amenazaba a la ciudad o al hogar se pensaba que era tan fácil de engañar por la figura del perro de paja, creyendo que era un perro guardián, y huía como si fuera un perro real. La práctica de colocar una estatua o imagen de un perro frente a su casa puede provenir de la costumbre de enterrar un perro de paja en el jardín de uno para protegerse contra el daño.
PERROS EN MESOAMÉRICA
Los mayas tenían una relación similar con perros como los chinos. Los perros fueron criados en corrales como una fuente de alimento, como guardianes y mascotas, y para la caza, pero también se asociaron con los dioses. Como los perros fueron notados como grandes nadadores, se pensó que llevaban las almas de los muertos a través de la extensión acuosa hacia la otra vida, el inframundo de Xibalba. Una vez que el alma llegó al reino oscuro, el perro sirvió como guía para ayudar al difunto a superar los desafíos presentados por los Señores de Xibalba y llegar al paraíso.
Esto se ha deducido de las excavaciones en la región que han descubierto tumbas en las que los perros son enterrados con sus maestros y de las inscripciones en las paredes del templo. Inscripciones similares en los Códices Mayas sobrevivientes describen al perro como el portador del fuego para las personas y, en el libro sagrado del Quiché Maya, el Popol Vuh, los perros son instrumentales en la destrucción de la ingrata e ingrata raza de humanos que los dioses produjeron por primera vez. y luego se arrepintió de.
Los aztecas y los tarascos compartieron esta visión del perro, incluido el perro como guía para la vida futura de los difuntos.Los aztecas también tenían una historia en su mitología con respecto a la destrucción de una primitiva raza de seres humanos en la que se presentan perros. En este cuento, los dioses ahogan el mundo en una gran inundación, pero un hombre y una mujer logran sobrevivir al aferrarse a un tronco. Una vez que las aguas retroceden, trepan a tierra firme y encienden un fuego para secarse. El humo de este fuego molesta al gran dios Tezcatlipoca, quien les arranca la cabeza y luego cose las cabezas en los extremos posteriores del hombre y la mujer y, al hacerlo, crea perros. De acuerdo con este mito, los perros son anteriores a la raza actual de los seres humanos y, por lo tanto, deben tratarse con respeto de la misma manera en que se trataría a un anciano. Los aztecas también enterraron perros con sus muertos y su dios de la muerte, Xolotl, fue imaginado como un enorme perro.
Los tarascos, como los aztecas y los mayas, tenían a los perros como mascotas, para cazar y para comer, y también los vinculaban con los dioses y la vida futura. Las almas de aquellos que murieron sin un entierro adecuado, como los que se ahogaron o se perdieron en la batalla o murieron solos en una cacería, fueron encontrados por perros espirituales que garantizarían su paso seguro a la otra vida. En las tres culturas (como, de hecho, en las otras mencionadas anteriormente), la creencia en los fantasmas era muy real. Un fantasma no solo podría crear problemas en la vida cotidiana de uno, sino que podría ocasionar daños físicos e incluso la muerte. El cuento tarasco sobre los perros espirituales disipó el temor de que, si uno no hubiera podido enterrar adecuadamente a un ser querido, el fantasma del difunto volvería a molestar a los vivos. La gente no debería temer porque el perro se encargaría del problema.
CONCLUSIÓN
En la India antigua, Mesopotamia, China, Mesoamérica y Egipto, la gente tenía lazos profundos con sus perros y, como se vio, esto también era común en la antigua Grecia y Roma. Los antiguos griegos pensaban en los perros como genios, como "poseer un cierto espíritu elevado". Platón se refirió al perro como un "amante del aprendizaje" y una "bestia digna de admiración". El filósofo Diógenes de Sinope amaba la simplicidad de la vida del perro y animaba a los seres humanos a emularlo. Mientras que otros animales han experimentado cambios significativos en la forma en que son percibidos a través de la historia (el gato, en particular) el perro ha sido un compañero constante, amigo y protector y ha sido portado de esa manera a través del arte y en las escrituras de muchos antiguos culturas. La antigua afirmación de que un perro es el mejor amigo se confirma a través del registro histórico, pero no necesita pruebas para nadie en la época moderna que tenga la suerte de disfrutar de la compañía de un buen perro.
Nota del autor: este artículo está dedicado a Sophia the Dog, mi verdadera filósofa.
LICENCIA:
Artículo basado en información obtenida de estas fuentes:con permiso del sitio web Ancient History Encyclopedia
El contenido está disponible bajo licencia Creative Commons: Attribution-NonCommercial-ShareAlike 3.0 Unported. Licencia CC-BY-NC-SA